Yanling Chang
Dynamic Discrete Choice Estimation with Partially Observable States and Hidden Dynamics
Aug 02, 2020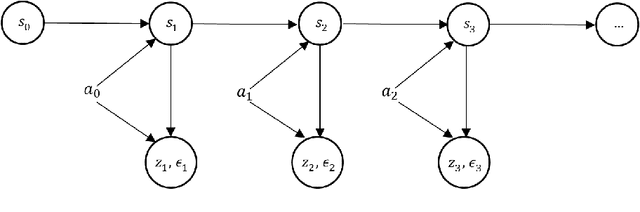


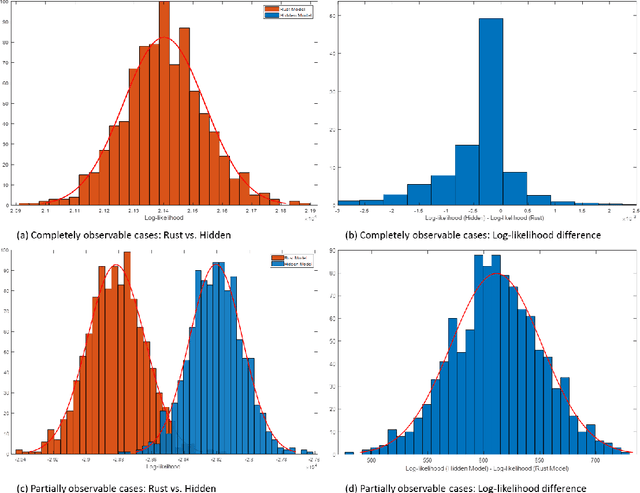
Abstract:Dynamic discrete choice models are used to estimate the intertemporal preferences of an agent as described by a reward function based upon observable histories of states and implemented actions. However, in many applications, such as reliability and healthcare, the system state is partially observable or hidden (e.g., the level of deterioration of an engine, the condition of a disease), and the decision maker only has access to information imperfectly correlated with the true value of the hidden state. In this paper, we consider the estimation of a dynamic discrete choice model with state variables and system dynamics that are hidden (or partially observed) to both the agent and the modeler, thus generalizing Rust's model to partially observable cases. We analyze the structural properties of the model and prove that this model is still identifiable if the cardinality of the state space, the discount factor, the distribution of random shocks, and the rewards for a given (reference) action are given. We analyze both theoretically and numerically the potential mis-specification errors that may be incurred when Rust's model is improperly used in partially observable settings. We further apply the developed model to a subset of Rust's dataset for bus engine mileage and replacement decisions. The results show that our model can improve model fit as measured by the $\log$-likelihood function by $17.7\%$ and the $\log$-likelihood ratio test shows that our model statistically outperforms Rust's model. Interestingly, our hidden state model also reveals an economically meaningful route assignment behavior in the dataset which was hitherto ignored, i.e. routes with lower mileage are assigned to buses believed to be in worse condition.
Partially Observed, Multi-objective Markov Games
Apr 16, 2014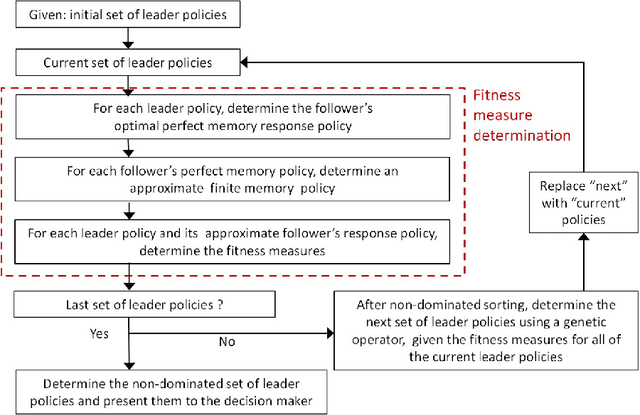
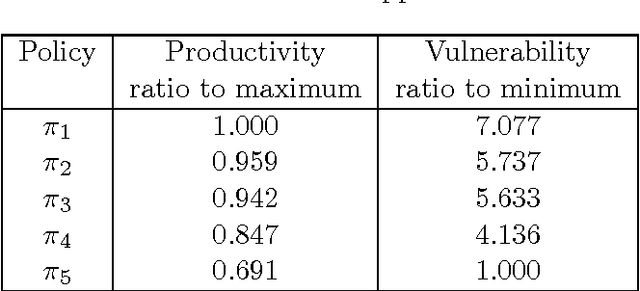
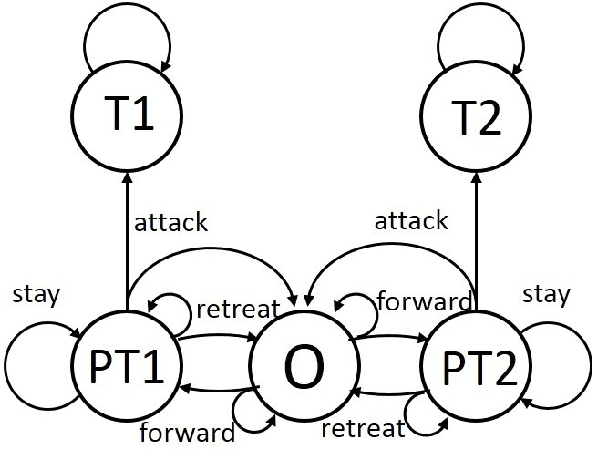
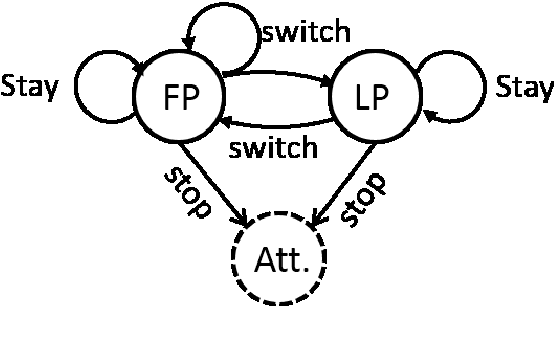
Abstract:The intent of this research is to generate a set of non-dominated policies from which one of two agents (the leader) can select a most preferred policy to control a dynamic system that is also affected by the control decisions of the other agent (the follower). The problem is described by an infinite horizon, partially observed Markov game (POMG). At each decision epoch, each agent knows: its past and present states, its past actions, and noise corrupted observations of the other agent's past and present states. The actions of each agent are determined at each decision epoch based on these data. The leader considers multiple objectives in selecting its policy. The follower considers a single objective in selecting its policy with complete knowledge of and in response to the policy selected by the leader. This leader-follower assumption allows the POMG to be transformed into a specially structured, partially observed Markov decision process (POMDP). This POMDP is used to determine the follower's best response policy. A multi-objective genetic algorithm (MOGA) is used to create the next generation of leader policies based on the fitness measures of each leader policy in the current generation. Computing a fitness measure for a leader policy requires a value determination calculation, given the leader policy and the follower's best response policy. The policies from which the leader can select a most preferred policy are the non-dominated policies of the final generation of leader policies created by the MOGA. An example is presented that illustrates how these results can be used to support a manager of a liquid egg production process (the leader) in selecting a sequence of actions to best control this process over time, given that there is an attacker (the follower) who seeks to contaminate the liquid egg production process with a chemical or biological toxin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge